De schaal van decibel [dB] voor A-gewogen geluidniveaus
Wat is een decibel?
De decibel [dB] geeft in de akoestiek de sterkte van het geluid aan, ofwel hoe hard een geluid is. Het is een lastige eenheid om voor de eerste keer te snappen. Er is een hoop theorie en context voor nodig. Toch zullen we proberen dit in 4 eenvoudige stappen uit te leggen.
-
- Geluid zijn trillingen
- Verschil vs verhouding
- Referentiewaarde van de decibel
- Logaritmische schaal voor geluidniveaus
1. Geluid zijn trillingen
Stel je voor: je staat in een volkomen stille kamer. In de verte laat iemand de lucht trillen met zijn stembanden door superzacht te fluisteren. Deze trillingen bewegen zich als rimpels door de lucht voort en gaat via je oor de gehoorgang binnen en brengt je trommelvlies heel zachtjes in beweging. De zwakste trillingen die ons oor theoretisch gezien als geluid kan waarnemen: een luchtdrukverschil van slechts 0,00002 pascal (Pa). Het tegenovergestelde: een straaljager die bulderend opstijgt, de straalmotor laat de lucht hevig trillen met een luchtdrukverschil van 200 Pa. Dit laat je trommelvlies zo hard trillen dat het pijn doet en het vlies zelfs kan scheuren. We kunnen horen van fluisterzacht tot pijnlijk hard.
2. Verschil vs verhouding
Het lastige van ons gehoor is het volgende: We horen niet het daadwerkelijke verschil tussen de trillingen, maar de verhoudingen.
Anders gezegd: we horen dat de trillingen 2x zo hard zijn geworden, niet dat er +1 Pa bijgekomen is. In onderstaande figuur zijn deze principes uitgewerkt.
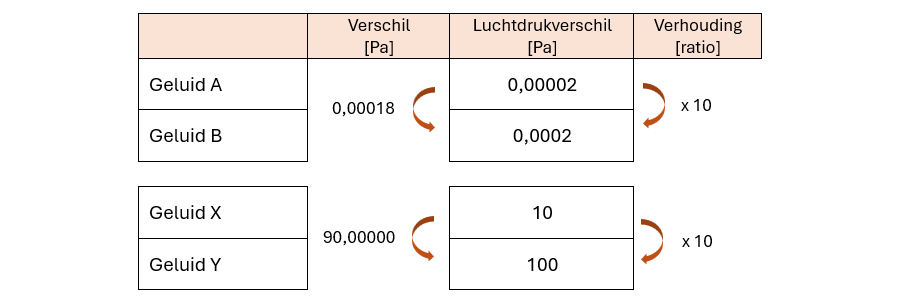
Tabel met verschil in luchtdruk vs verhouding in luchtdruk
- Geluid A en B verschillen 0,00018
- Geluid X en Y verschillen 90
- De verhoudingen tussen A en B is gelijk aan X en Y (x10)
- Het verschil tussen geluid A en B is voor je gehoor gelijk aan X en Y
3. Referentiewaarde van de decibel
De decibel is een puntentelling voor de verhouding van een onderliggende waarde. Je zou de regel voor het omrekenen van luchtdruk naar decibel als volgt kunnen omschrijven:
Als de geluiddruk [Pa] (onderliggende waarde) x10 vermenigvuldigd (verhouding), komen er 20 punten op de decibelschaal bij (puntentelling).
Omdat de decibel een verhouding is heb je een beginwaarde nodig om je gemeten waarde mee te vergelijken. Dit noemen we de referentiewaarde of een indexwaarde. Het is de basis van de schaal waar elke gemeten waarde mee vergeleken wordt. Voor een gemeten geluidniveau dB(A) is dat meestal de ondergrens van ons gehoor:
0,00002 Pa (pascals), kun je ook schrijven als 2 µPa (micropascals)
4. Logaritmische schaal voor geluidniveaus
Een decibel maakt gebruikt van een logaritme voor de puntentelling. Binnen de akoestiek zijn er twee logaritme om de decibel te berekenen. Zonder in te gaan op de verschillen en wanneer je welke moet gebruiken geven we ze hieronder.
a) 20*log10(a1/a2)
b) 10*log10(b1/b2)
Logaritme a kunnen we gebruiken om geluiddruk (Pa) om te rekenen naar geluidniveau (dB). Vermenigvuldigd de luchtdruk met x10, dan komen er 20 punten op de schaal van decibel bij.
Een geluidmeter berekend op vergelijkbare manier geluidniveaus:
- Meting van het luchtdrukniveauverschil= 200 Pa
- Vergelijkt dat met de referentiewaarde = 0,00002 Pa
- Berekent de verhouding tussen beide waarden en zet ze op de logaritmische schaal: 20log10(gemeten niveau/referentieniveau)
- In Excel kun je dit zelf invoeren als =20*LOG10(200/0,00002) geeft 140 dB.
Dit principe is onderstaande figuur weergegeven met een tabel van verschillende geluidbronnen met de bijbehorende geluiddruk en geluidniveaus. In de grafiek zie je dezelfde waarden grafisch uitgebeeld. Met beide waarden aan weerszijde van de Y-as.
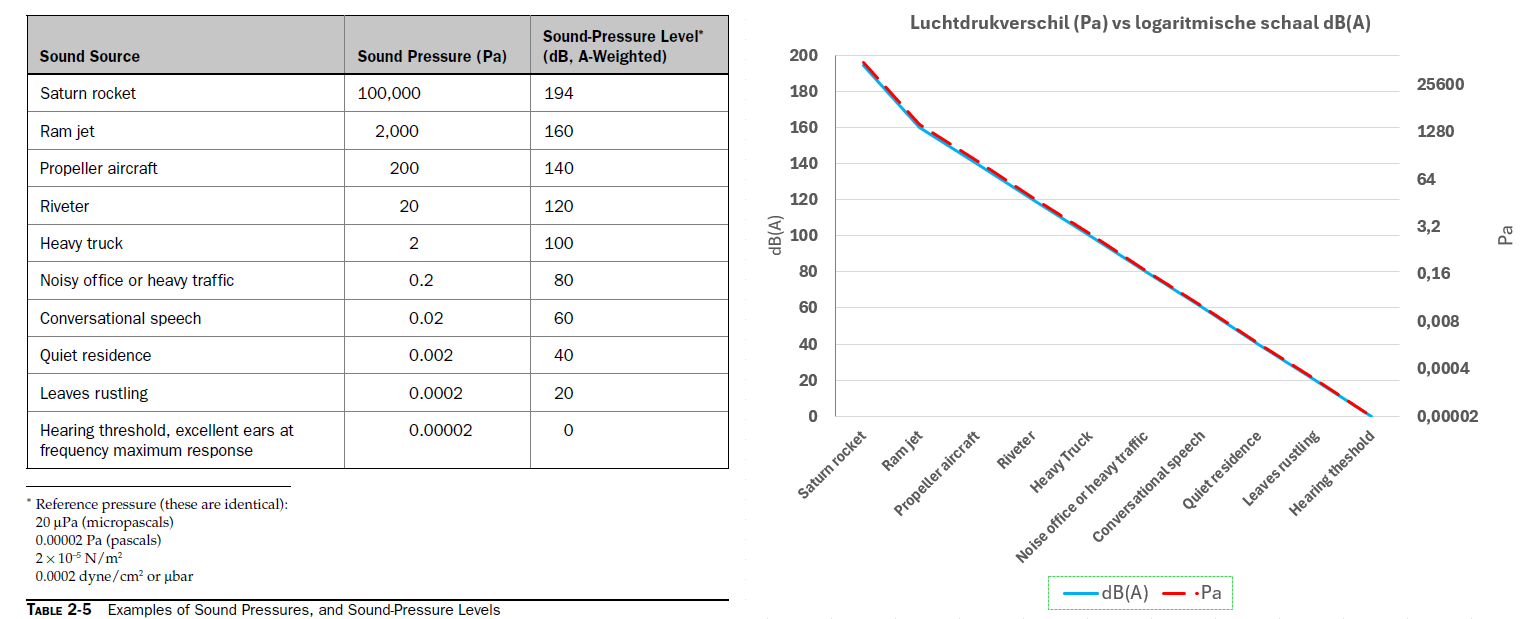
Verschillende geluidbronnen in luchtdrukverschillen (Pa) en het geluiddrukniveau (dB) (bron: Master Handbook of Acoustics en eigen grafiek)
Het optellen van decibels
Door deze logaritmische schaal kun je geluidniveaus niet altijd optellen met de ‘+’ op je rekenmachine. Een rekenvoorbeeld:
Je zet een luidspreker aan en je meet 40 dB(A) muziekgeluid. Je verdubbeld het vermogen van de versterker, hoeveel dB klinkt er nu?
Hierbij moet je de logaritme blijven gebruiken op onderliggende waarden, in dit geval het bronvermogen, met de volgende rekenregel = 10*log10(b1+b2). Waaruit blijkt dat het juiste antwoord 40 dB + 40 dB = 43 dB.
Een metafoor met fietsen is wellicht eenvoudiger te begrijpen.
Henk en Ingrid fietsen elk op hun eigen fiets 20 km/u. Ze gaan met dezelfde inspanning samen trappen op een tandem, hoe hard denk je dat ze nu rijden? Het antwoord zal dichter bij de 23 dan 40 km/u liggen.
Grappig weetje: omdat 0 dB(A) alleen maar de referentiewaarde uitdrukt, kan er ook -1 dB(A) zijn. Dit kunnen wij mensen misschien niet horen, maar je kunt het wel meten. Daarom geld ook dat 0 dB(A) + 0 dB(A) = 3 dB(A) kan zijn. Meer over de decibel en hoeveel geluid afneemt per meter lees je in ons blog over de afname van geluid.

Verdubbeling van vermogen geeft geen verdubbeling van de snelheid of geluidniveau
NB. Als er wetenschappelijke nuances verloren gaan is dat om het principe vereenvoudigd uit te leggen. Zie je een verbeterpunt? Laat het alsjeblieft weten in de comments onderaan deze blog.
Wie heeft de decibel uitgevonden?
De schaal van de decibel is verzonnen door meneer Alexander Graham Bell (die van je telefoon en het werkwoord “bellen”). Oorspronkelijk voor elektronische telefoonsignalen, maar het bleek ook handig voor geluid. Een decibelwaarde zonder onderliggende waarde betekent niets. Daarom wordt het ook wel een ‘pseudo-eenheid’ genoemd.
In geluid heb je bijvoorbeeld het bronvermogen van een elektrisch apparaat (Lw), een geluidniveau in een ruimte (SPL) en de geluidintensiteit (IL). Allen worden in dB’s uitgedrukt, ze betekenen allemaal wat anders.
GOED Deze grasmaaier produceert een brongeluidniveau van LwA = 95 dB
FOUT Dit product helpt 6 dB


0 Comments