
Mayan Warrior Soundsystem @ Burning man. bron: researchgate.com
Hoe gedraagt geluid zich in een open veld? In deze blog gaan we je alles leren over de afname van geluid. Naarmate de blogs vorderen zullen we meer technische aspecten gaan behandelen, we doen ons best het onderwerp zo eenvoudig mogelijk te blijven beschouwen.
De afname over afstand van een puntbron
Stel je voor, je staat op een lege landingsbaan van Schiphol. We staan op een paar meter afstand van een geluidbron. Deze bron staat op ooghoogte. De bron straalt rondom flink wat geluid uit. De bron van een geluid noemen we ook wel het emissiepunt (Latijn: ēmissio ‘het uitzenden, loslaten’). In het begin is het niet groter dan de bron zelf, maar dat duurt niet lang. Met de snelheid van geluid (circa 335 m/s) breidt de schokgolf steeds verder uit over de landingsbaan. Net zolang tot het ons oor bereikt en ons trommelvlies in beweging brengt, nu horen we het geluid. Zolang de ‘explosie van geluid’ zich uitbreidt, is er steeds meer oppervlak waarover de energie wordt ‘uitgesmeerd’. De kracht zal naarmate de afstand tot de bron groter wordt dus afnemen. Conclusie, een geluidbron klinkt zachter naarmate hij verder van je vandaan staat. In onderstaande afbeelding is het zwakker worden van het geluidniveau naarmate je verder van de bron gaat staan uitgebeeld.

Op verschillende afstanden van de geluidbron is het geluidniveau gemeten. Het ontvangpunt/beoordelingspunt heet ook wel een imissiepunt (het omgekeerde van emissie). De afstand van de meting hebben we elke keer verdubbelt (r, 2*r, 4*r, 8*r, …). De uitkomsten zijn in onderstaande grafiek weergegeven.
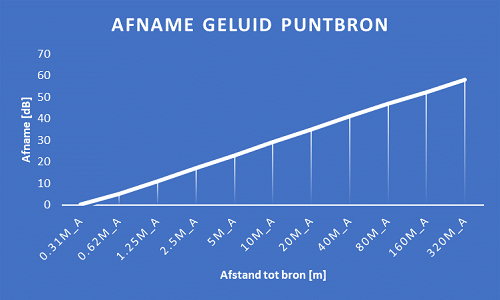
We weten uit ons eerdere blog over decibellen dat een verdubbeling van het geluidniveau 3 dB is (1+1 = 4dB). Een logische hypothese zou kunnen zijn dat met de verdubbeling van de afstand (r*2) het geluidniveau halveert (dB/2) en dus weer met 3 dB afneemt. Zullen we kijken of dat klopt?
In bovenstaande grafiek lezen we af dat het geluid met 60 dB in 10 stappen afneemt. Voor elke verdubbeling van de afstand (r*2) is dat 6 dB afname (60/10) en dus geen 3 dB zoals onze hypothese voorspelde. Hoe komt dit? Herinner je de opmerking over de groter wordende bol (schokgolf van de explosie)? Het oppervlak waarover de energie wordt uitgesmeerd is driedimensionaal en niet tweedimensionaal zoals de eerste afbeelding doet vermoeden. In onderstaande figuur is een illustratie van dit principe te zien. De energie wordt uitgesmeerd in zowel de horizontale als de verticale richting.
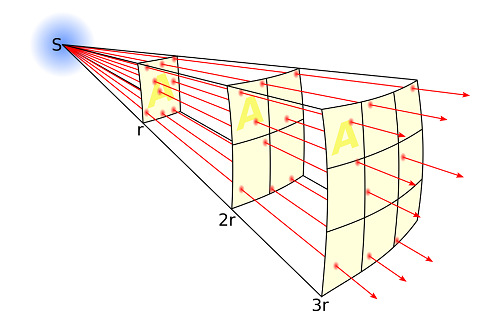
bron: Wikipedia
Je ziet in de afbeelding bij de eerste afstand r een oppervlak A. Bij de volgende verdubbeling van de afstand 2r is het oppervlak A in 2 richtingen groter geworden. Het verschil tussen afstand r en 2r (1:2) geeft een verschil van oppervlak A en 4A (1:4). Dit heet de omgekeerde kwadratenwet. Een vermindering van de energie met een factor 4 staat gelijk aan 6 dB. Bij een puntbron geeft een verdubbeling van de afstand dan ook een afname van 6 dB. Dit is een handige vuistregel in de akoestiek. Andersom geldt hij ook, een halvering van de afstand tussen jou en de puntbron geeft een toename van 6 dB.
De afname over afstand van een lijnbron
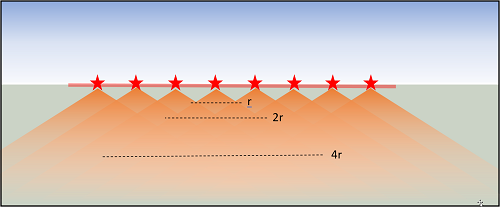
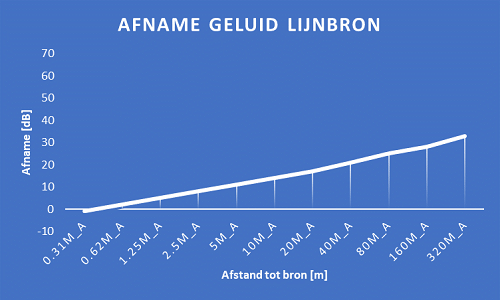
Nu nemen we dezelfde geluidbron uit bovenstaand verhaal, maar we zetten er een heleboel naast elkaar totdat zich een lijn van bronnen vormt over de breedte van de landingsbaan. In ons zichtveld zien we geen puntbron maar een lijnbron zoals in onderstaande afbeelding. De grafiek laat weer de afname zien per verdubbeling van de afstand. En wat zie je? Er vindt na 10 stappen een afname van totaal 30 dB plaats. Als je wegloopt van de ene puntbron kom je namelijk steeds weer in de invloedssfeer terecht van de puntbron ernaast. Kijk maar naar de afbeelding met de uitstraling van alle bronnen op een rij. Bij een lijnbron geeft een verdubbeling van de afstand (r) een afname van 3 dB.
Breinkraker
Je staat op 1 meter afstand voor een geluiduitstralend vlak van 20 x 10 meter en houdt je microfoon 5 meter in de lucht (met een statief bijvoorbeeld). Als je nu een meter naar achter loopt (of twee of zelfs 3) is de afname ongeveer 0 dB. Je staat nog in de ‘directe invloedsfeer’ van het uitstralende vlak waardoor er geen afname plaatsvindt.

Dus wat hebben we geleerd:
- Als je voor een groot vlak staat dat geluid uitstraalt en je hele blikveld inneemt, zal het geluidniveau bij het vergroten van je afstand tot de bron niet tot nauwelijks afnemen.
- Wanneer de geluidbron eruitziet als een lijn aan de horizon neem het geluidniveau met elke verdubbeling van de afstand 3 dB af.
- Als je geluidbron een stip op je horizon vormt neemt het geluid met elke verdubbeling van de afstand 6 dB af.

Goedemiddag,
Ik heb met belangstelling uw blog gelezen over geluid in de vrije ruimte.
Nu vraag ik mij af op welke afstand vanaf de geluidsbron, een lijnbron met een lengte van bv 50 m overgaat in een puntbron.
Is er een relatie tussen de lengte van een lijnbron en de afstand tot het immissiepunt om de lijnbron te behandelen als een puntbron?
Dag Kees,
Daarvoor kunnen we het best aansluiting vinden bij de Handleiding meten en rekenen Industrielawaai (HMRI).
Daarin staat het volgende:
Een lijnbron met een lengte van 50 m heeft ook snel een diameter van circa 50 m. Ik geloof niet dat de bron heel hoog is?
Hier zou gelden dat 1,5 * d = 1,5 x 50 = 75 m
Let op, bij > 50m afstand moet je corrigeren voor meteocorrectie (weersinvloeden). Ook dit is terug te vinden in de HMRI, wellicht voor deze exercitie te uitgebreid.
Als je indicatief een meting wil uitvoeren kun je met een lichte wind mee (richting de meting) een geluidniveau bepalen.
succes!